Graf - Matematika Diskrit

GRAF

Sejarah graf dimulai dengan masalah jembatan Konigsberg (tahun 1736) yaitu dengan muncul pertanyaaan melalui setiap jembatan tepat sekali dan kembali lagi ke tempat semula?

Graf jembatan Konigsberg terdiri dari :

· Simpul (vertex)untuk menyatakan daratan

· Busur  (edge)untuk menyatakan jembatan

Euler menjelaskan bahwa tidak mungkin seseorang berjalan melewati tepat satu kali masing-masing jembatan dan kembali lagi ke tempat semula. Hal ini disebabkan karena pada graf model jembatan Königsberg itu tidak semua simpul berderajat genap.

Pengertian Graf

Graf  G  merupakan  sebagai pasangan himpunan (V,E), yang ditulis dengan notasi G = (V, E), yang artinya :

·         V  adalah himpunan tidak kosong dari simpul-simpul (vertices)  = { v₁ , v₂ , ... , v_n }

·         E adalah himpunan busur/sisi  (edges) yang menghubungkan   sepasang  simpul  = {e₁ , e₂ , ... , e_n }

Contoh 

G₁ adalah graf dengan V = { 1, 2, 3, 4 } dan  E =  { (1, 2), (1, 3), (2,3), (2, 4), (3, 4) }

Secara gemoteri graf memiliki arti sebagai sekumpulan noktah (simpul) di dalam bidang dwimatra yang dihubungkan dengan sekumpulan garis (sisi). 

    graf sederhana                   graf ganda                       graf semu

Jenis - Jenis Graf

Berdasarkan ada atau tidaknya gelang atau sisi ganda pada suatu graf, maka graf digolongkan menjadi dua jenis,yaitu:

·        1.Graf sederhana (simple graph)

         Adalah graf yang tidak mengandung  gelang maupun sisi-ganda

·        2.Graf tak-sederhana (unsimple-graph).

         Adalah graf yang mengandung sisi ganda atau gelang.

contoh:

                     

Jenis-Jenis Graf berdasarkan orientasi arah

Berdasarkan orientasi arah pada sisi, maka secara umum graf  dibedakan atas 2 jenis:

·    A.Graf tak-berarah (undirected graph)

Adalah graf yang sisinya tidak mempunyai orientasi arah.

·    B.Graf berarah (directed graph atau digraph)

Adalah graf yang setiap sisinya diberikan orientasi arah .

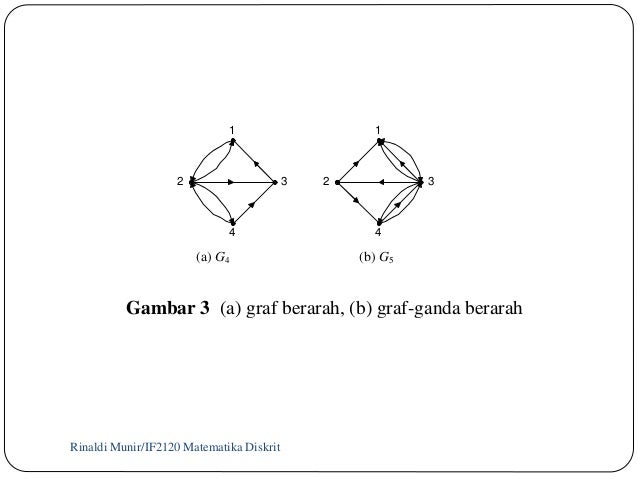
Terminologi Graf

A. Ketetanggaan (Adjacent)

Dua buah simpul disebut bertetangga bila kedua simpul terhubung langsung.

Contoh 

Tinjau graf G₁ :

·  simpul 1 bertetangga dengan simpul 2 dan 3

·  simpul 1 tidak bertetangga dengan  simpul 4.

G1

B. Bersisian (Incidency)

Untuk sembarang sisi e = (v_j, v_k) diebut e bersisian dengan simpul v_j , atau e bersisian dengan simpul v_k

Contoh 

Tinjau graf G₁:

· sisi (2, 3) bersisian dengan simpul 2  dan simpul 3

· sisi (1, 2) tidak bersisian dengan simpul 4.

C. Simpul Terpencil (Isolated Vertex)

Simpul terpencil adalah simpul yang tidak mempunyai sisi yang bersisian dengannya.

Contoh 

Tinjau pada  graf G₃: simpul 5 merupakan simpul terpencil.

D. Graf  Kosong (null graph atau empty graph)

Adalah graf yang himpunan busurnya merupakan himpunan kosong (N_n).

E. Derajat (Degree)

Derajat suatu simpul adalah jumlah sisi yang bersisian dengan simpul tersebut. Notasi yang digunakan  adalah d(v)

Contoh 

 Tinjau graf G₁:     

·         d(1) = d(4) = 2

·         d(2) = d(3) = 3

Contoh 

Tinjau graf G₂:

·         d(1) = 3 → bersisian dengan sisi ganda          

·         d(3) = 4 → bersisian dengan sisi gelang (loop)

G 2

Contoh 

Tinjau graf G₃:

· d(5) = 0   → simpul   terpencil

· d(4) = 1  → simpul anting-anting (pendant vertex)

 

F. Derajat Graf Berarah

Pada sebuah graf berarah maka

·  d_in(v)       = derajat-masuk (in-degree)   = jumlah busur yang masuk ke simpul v

·  d_out(v)      = derajat-keluar (out-degree )  = jumlah busur yang keluar dari simpul v

·  d(v)         = d_in(v) + d_out(v)                                                                                    

Contoh 

Tinjau graf G₄:

d_in(1) = 2;               d_out(1) = 1

d_in(2) = 2;               d_out(2) = 3

d_in(3) = 2;               d_out(3) = 1

d_in(4) = 1;               d_out(3) = 2

G. Lemma Jabat Tangan

Jumlah derajat semua simpul pada suatu graf adalah genap adalah dua kali  jumlah busur pada graf tersebut. 

Dengan kata lain, jika G = (V, E), maka:

 

Contoh 

Tinjau graf G₁: 

d(1) + d(2) + d(3) + d(4) = 2 + 3 + 3 + 2 = 10

G

Contoh 

Tinjau graf G₂: 

d(1) + d(2) + d(3) = 3 + 3 + 4 = 10

G2

H. Lintasan

Lintasan yang dimana panjangnya n dari simpul awal v₀ ke simpul tujuan v_n didalam graf G ialah barisan berselang-seling simpul-simpul dan sisi-sisi yang berbentuk v₀, e₁, v₁, e₂, v₂,... , v_n –1, e_n, v_n sedemikian sehingga e₁ = (v₀, v₁), e₂ = (v₁, v₂), ... , e_n = (v_n-1, v_n) adalah sisi-sisi dari graf G.

Contoh 

Tinjau graf G₁: lintasan 1, 2, 4, 3 adalah lintasan dengan barisan sisi (1,2), (2,4), (4,3). Panjang lintasan adalah jumlah sisi dalam lintasan tersebut. Lintasan 1, 2, 4, 3 pada G₁ memiliki panjang 3.

Pada prinsipnya simpul dan sisi yang dilalui di dalam lintasan boleh berulang. Sebuah lintasan dikatakan Lintasan Sederhana (simple path) jika semua simpulnya berbeda (setiap sisi dilalui hanya satu kali). Lintasan yang berawal dan berakhir pada simpul yang sama disebut lintasan Tertutup (close path). Lintasan yang tidak berawal dan berakhir pada simpul yang sama disebut lintasan terbuka (open path). Coba perhatikan pada G₁lintasan:

·        1,2,4,3           → lintasan sederhana dan  lintasan terbuka

·        1,2,4,3,1       → lintasan sederhana dan lintasan tertutup

·        1,2,4,3,2       → bukan lintasan sedernana tetapi lintasan terbuka

Sirkuit

Sirkuit atau siklus adalah lintasan yang berawal dan berakhir pada simpul yang sama . Coba kita tinjau graf G₁: 1, 2, 3, 1 adalah sebuah sirkuit.

Panjang sirkuit adalah jumlah sisi dalam sirkuit tersebut. Sirkuit 1, 2, 3, 1 pada G₁ memiliki panjang 3

Representasi Graph

1. Matriks Ketetanggaan  

                            (adjacency matrix)

2. Matriks Bersisian  

                            (incidency matrix) 

3. Senarai Ketetanggaan  

                            (adjacency list)

Matriks Ketetanggaan (adjacency matrix)

A = [aij],

                1, jika simpul i dan j bertetangga

aij = {

                0, jika simpul i dan j tidak

                bertetangga.

Matriks Bersisian (incidency matrix)

A = [aij],

    1, jika simpul i bersisian dengan sisi j

aij = {

     0, jika simpul i tidak bersisian dengan

     sisi j

SubGraf dan Komplemen

Misalnya G = (V, E) adalah sebuah graf. G1 = (V1, E1) adalah SubGraf dari G jika V1 Í V dan E1 Í E. Komplemen dari SubGraf G1 terhadap graf Gadalah graf G2 = (V2, E2) sedemikian sehingga E2 = E - E1 dan V2 adalah himpunan simpul yang anggota-anggota E2 bersisian dengannya.

Contoh 

Perhatikan Graf G₁

                                Graf G1             SubGraf G1      bukan Subgraf G1

I. SubGraf Rentang

SubGraf G₁ = (V₁, E₁) dari G = (V, E) dikatakan SubGraf rentang jika V₁=V (yaitu G₁ mengandung semua  simpul dari G).

                                                Graf              Subgraf Rentang    Bukan subgraf rentang

J. Cut-Set

Cut-set dari graf terhubung G adalah himpunan sisi yang bila dibuang dari G menyebabkan G tidak terhubung. Jadi, cut-set selalu menghasilkan dua buah komponen. Terdapat banyak cut-set pada sebuah graf terhubung.

Contoh 

Pada graf di bawah, {(1,2), (1,5), (3,5), (3,4)} adalah cut-set. Himpunan {(1,2), (2,5)} juga adalah cut-set, {(1,3), (1,5), (1,2)} adalah cut-set, {(2,6)} juga cut-set, {(1,2), (2,5), (4,5)} bukan cut-set sebab himpunan bagiannya, {(1,2), (2,5)} adalah cut-set.

K. Graf Berbobot

Graf berbobot adalah graf yang setiap sisinya diberi sebuah bobot

Contoh 

Lintasan dan Sirkuit

Berikut ini akan diperkenalkan lintasan dan sirkuit Euler dan Hamilton

A. Lintasan dan Sirkuit Euler

Lintasan Euler ialah lintasan yang melalui masing-masing sisi di dalam graf tepat satu kali. Sirkuit Euler ialah sirkuit yang melewati masing-masing sisi tepat satu kali. Graf yang mempunyai sirkuit Euler disebut graf Euler (Eulerian graph). Graf yang mempunyai lintasan Euler dinamakan juga graf semi-Euler (semi-Eulerian graph).

B. Lintasan dan Sirkuit Euler Pada Graf Tidak Berarah

Graf tidak berarah memiliki lintasan Euler jika dan hanya jika

·         -Terhubung

·         -Memiliki dua buah simpul berderajat ganjil

·         -atau setiap simpul berderajat genap.

Graf tidak berarah G memiliki sirkuit Euler (Graf Euler) jika dan hanya jika setiap simpul berderajat genap.

Contoh 17

Jika diketahui Graf berikut ini

Maka lintasan Eulernya adalah

1. 3, 1, 2, 3, 4, 1
2. 1, 3, 2, 1, 4, 3

Sebagai catatan Graf tersebut memiliki 2 buah simpul berderajat ganjil (simpul 1 dan 3)

Contoh 18

Jika diketahui Graf berikut ini

Maka sirkuit eulernya adalah 1, 2, 3, 4, 7, 3, 5, 7, 6, 5, 2, 6, 1

Sebagai catatan, graf tersebut  Setiap simpulnya berderajat genap

C. Lintasan &  Sirkuit Hamilton

Lintasan Hamilton ialah lintasan yang melalui tiap simpul di dalam graf tepat satu kali. Sirkuit Hamilton ialah sirkuit yang melalui tiap simpul di dalam graf tepat satu kali, kecuali simpul asal (sekaligus simpul akhir) yang dilalui dua kali. Graf yang memiliki sirkuit Hamilton dinamakan Graf Hamilton, sedangkan graf yang hanya memiliki lintasan Hamilton disebut Graf Semi-Hamilton.

(a)                        (b)                          (c)

Perhatikan pada Gambar di atas bahwa Graf:

(a) graf yang memiliki lintasan Hamilton (misal: 3, 2, 1, 4)

(b) graf yang memiliki sirkuit Hamilton (1, 2, 3, 4, 1)

(c)  graf yang tidak memiliki lintasan maupun sirkuit Hamilton

Representasi Graph

     1. Matriks Ketetanggaan (adjacency matrix)
2. Matriks Bersisian  (incidency matrix) 
3. Senarai Ketetanggaan  (adjacency list)
Matriks Ketetanggaan (adjacency matrix)
A = [aij],
                1, jika simpul i dan j bertetangga
aij = {
                0, jika simpul i dan j tidak
                bertetangga.

Matriks Bersisian (incidency matrix)
A = [aij],
    1, jika simpul i bersisian dengan sisi j
aij = {
     0, jika simpul i tidak bersisian dengan
     sisi j

Graph Isomorfik

Menurut geometri, dua gambar disebut kongruen apabila keduanya mempunyai sifat-sifat geometri yang sama. Apabila caranya sama, dua graf dapat disebut isomorfis jika keduanya menunjukkan "bentuk" yang sama, kedua graph tersebut hanya berbeda dalam hal pemberian label titik dan garisnya saja.

Syarat dua buah graph dikatakan isomorfik, yaitu :

1. Memiliki jumlah simpul yang sama
2. Memiliki jumlah garis yang sama
3. Memiliki derajat yang sama dari simpul-simpulnya

Catatan : Jika dua graph yang berbeda tidak memiliki salah satu dari syarat diatas sudah dapat dipastikan kedua graph tersebut tidak isomorfis, tetapi walaupun kedua graph tersebut memiliki seluruh syarat diatas belum tentu juga keduanya isomorfis.

Ada dua graf yang memenuhi tiga syarat tersebut, tetapi keduanya tidak isomorfis.Contohnya adalah graf G dan G' pada Gambar di bawah ini :

Dalam G, satu-satunya titik yang berderajat 3 adalah titik x. Titik x dihubungkan dengan 2 titik lain yang berderajat 1 (titik y dan z). Sebaliknya, dalam G', satu-satunya titik yang berderajat 3 adalah c. Satu-satunya titik berderajat 1 yang dihubungkan dengan c hanyalah titik d, sehingga G tidak mungkin isomorfis dengan G'.

Untuk itu ada beberapa syarat tambahan yang wajib kita penuhi apabila ingin menunjukkan apakah kedua graph tersebut isomorfik atau tidak, yaitu :

1. Graf sederhana G₁ = (V₁, E₁) dan G₂ = (V₂, E₂) adalah  isomorfis jika ada sebuah fungsi bijektif (fungsi satu-ke-satu dan on to) dari V₁ ke V₂ dengan sifat kepemilikan bahwa jika a dan b adalah tetangga pada G₁ jika dan hanya jika  f(a) dan f(b) adalah tetangga di G₂, untuk seluruh  a dan b di V₁.
2. Misalkan sisi e bersisian dengan simpul u dan v di G₁, maka sisi e’ yang berkoresponden di G₂ harus bersisian dengan simpul u’ dan v’ yang di G₂.
3. G₁ dan G₂ adalah isomorfis jika simpul-simpulnya dapat diurut  dengan cara sedemikian rupa sehingga matriks adjacensy M_G1 dan M_G2 adalah identik.

Agar lebih mudah memahami apakah dua graf isomorfik atau tidak, berikut adalah contoh cara menunjukan dua graf yang isomorfik.

CONTOH 1 :

Periksa apakah kedua graf tersebut isomorfik? Jika ya, tentukan simpul-simpul yang saling berkorespondensi antara G₁ dan G₂

penyelesaian:

Ya,  kedua graf tersebut adalah isomorfik. Terlihat graf tersebut memuat simpul dimana setiap simpulnya masing-masing berderajat tiga. Simpul yang saling berkorespondensi dari kedua graf tersebut adalah :

simpul u1 berkorespondensi dengan simpul v1

simpul u2 berkorespondensi dengan simpul v3

simpul u3 berkorespondensi dengan simpul v5

simpul u4 berkorespondensi dengan simpul v6 

simpul u5 berkorespondensi dengan simpul v4

simpul u6 berkorespondensi dengan simpul v2

Pada dua graf yang isomorfik, kedua graf tersebut memiliki matriks ketetanggaan yang sama, tentunya setelah matriks yang berkorespondensi diurutakan dalam urutan yang sama.

Perhatikan matriks ketetanggaan dari kedua graf  tersebut. Dibawah ini adalah matriks ketetanggaan dari graf G₁ dan G₂:

Terlihat bahwa kedua graf  tersebut  memiliki  matriks  ketetanggaan  yang  sama,   yaitu  M_G1 =  M_G2.